Source (restricted to non-HBO-Max regions)
Kamala Harris is known to love Venn diagrams and would be cringing hard at this.
For reference, circles in Venn (Euler) diagrams are sets of objects with a certain property. Select objects are shown inside or outside of each circle depending on whether they belong to the set.
A good example is xkcd 2962:
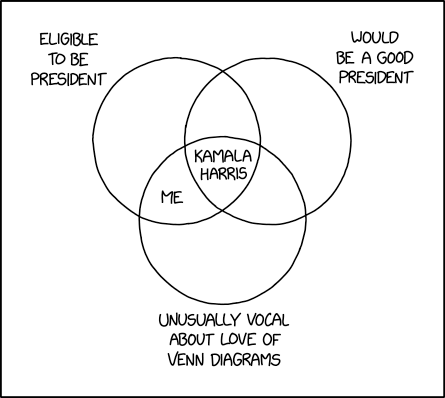
Can someone explain what part he’s incorrect about? (Since we’re in ConfidentlyIncorrect)
A correct Venn diagram of “KAMA” and “BLA” would have only “A” in the middle, because that is the only part that is present in both.
If we assume it’s about letters, then the sets would need to be like
( KM ( A ) BL )No, because A is not part of KM or of BL. The intersection is supposed to show what both sets have in common.
I am correct if we assume
- Left set: “Letters in ‘KAMA’”
- Right set: “Letters in ‘BLA’”
The exclusive region of the left set will only contain K and M. The left set will contain K, M and A, the last one is also a member of the right set.
Oh, now i get what you meant. Sorry, I misunderstood.
Which part of the tweet did you think was right?

Maybe I should ask OP who it is they’re saying is confidently incorrect? I originally thought that they were saying Oliver was incorrect, but your response makes me wonder if they meant the Trump campaign response was incorrect.
Basically, I just want clarification.
I’m not saying either is good use of Venn diagrams (as opposed to the provided xkcd comic). A better “mathematical” way to express the relation is simply “KAMA + BLA = KAMABLA” (yes, the mathematical sign “+” is not used for concatenation in math but you get the point).
The tweet would work if we assume:
- Left set A contains words that include “KAMA”, notably “KAMA” itself
- Right set B contains words that include “BLA”, notably “BLA” itself
- Their intersection A ∩ B contains words that belong to both sets, notably “KAMABLA”.
Is it a technically correct Venn diagram? I’d say it could be, given the above weird assumptions.
Is a Venn diagram the correct tool for the job? No.As for JO’s example with sea creatures: if we assume
- A is a set of dolphins
- B is a set of sharks
- their intersection is an empty set: A ∩ B = { } because no dolphins are sharks
JO’s example might work if
- A was a set of properties of dolphins
- B was a set of properties of sharks
- their intersection includes “lives in the ocean”: A ∩ B = {“lives in the ocean”, …} because “lives in the ocean” is both a property of dolphins and a property of sharks
However, this essentially turns around the convention “sets are defined by properties and include objects” to “sets are defined by objects and include their properties”, which is in my opinion even more cringey than considering “words containing ‘BLA’” a notable set. (From a mathematical standpoint. The entire “Kamabla” thing is pure cringe in the practical sense.)
I think this is a good explanation of why JO is wrong, which I was not expecting.
As for JO’s example with sea creatures: if we assume
- A is a set of dolphins
- B is a set of sharks
- their intersection is an empty set: A ∩ B = { } because no dolphins are sharks
This was my exact thought as I was watching but totally let it pass when he gave his “solution” without another thought before now.
However I still don’t think the tweet works. Your logic is sound but the diagram would need to label sets A and B with “Words that include…”
Of course that would just further expose it as unfunny and pointless.
ETA: I notice you edited the comment while I was replying. Hoping you didn’t change the substance too much - I don’t have time at the moment to figure out what changed and see if my response still applies 😅🤞
It’s certainly not very useful or informative.
But please explain how it is incorrect.
In a Venn diagram, the overlap is what the individual areas have in common. It’s the intersection, not the union.
Well for starters Kamabla is not actually at the intersection of Kama and Bla…

You have two strings and in the overlap you have the concatenated string formed from the parts. Again, not useful but a totally valid interpretation.
So … can you actually explain why you think it is incorrect or is snarky comments all you got?
This article on Intersection might help you understand
Here are the basics, though:
The intersection of
and
is the set
of elements that lie in both set
and set
That picture does not make it clear that the labels refer to regions, not elements. A clearer explanation of set operators is the following:

- B (Set B)
- A ∪ B (Union of A and B)
- A (Set A)
- A \ B (A minus B; notation varies)
- B \ A (B minus A)
- A ∩ B (Intersection of A and B)
What relation function matches your interpretation?
Since you’re the Venn diagram expert now…
The kamabla in the middle suggests that both kama and bla have kamabla in it, since that’s what they have in common. But kama doesn’t have bla, and bla doesn’t have kama. So they should not overlap. Hope that makes sense.
but that what I remember him saying.
I’m not sure what that has to do with Venn diagrams.
Guess this is the difference between chart bitches and diagram enjoyers.
Chart bitches be like: “The y-axis does not start at 0! Misleading!”
Diagram enjoyers be like: “It mathematically cannot because it’s a logarithmic scale, which is the only way this data can be reasonably visualized; but I suppose they should have made the y-labels bigger and add minor horizontal gridlines so even people like you notice that.”
can’t we just enjoy an absurdist joke here
If he was a mathematician with an audience of mathematicians that all knew this was wrong, the error could have worked as an extra intentional joke. However, the joke he went for could have been made without this error.
Basically, this is an unforced mistake that ruined a joke for some while having little to no effect on others’ enjoyment of it. You’re in the latter group and I recognize there is a significant number of you in JO’s live audience as well as on Lemmy, as this post is quite controversial.
This guy has a very punchable face and is insufferable. I don’t understand how he is so popular.
It turns out funny news with lots of bias is a winning combination
But he is not funny…
Other Team Bad is objectively hilarious, you are incorrect
What if I’m in neither teams? I’m European.
Look it’s okay if you have no humor, but don’t judge other people for it, okay?
The funny thing about this statement is that it’s something John would say about himself
The funny thing about this statement is that it’s something John would say about himself
If you talk fast enough and are self deprecating its funny.
He has a live audience so he (and the writing team) knows what’s funny, and limits self-deprecation to about twice per episode. The show mostly features more conventional joke material (references to pop culture, defying expectations, reframing events in surprising context).
Its even funnier when you explain it.
It’s ok if the humour isn’t for you
You are correct. Self-deprecation is overdone in this corner of the internet so we’ve grown numb to it, while a live or TV audience largely hasn’t, as evidenced by the laughter. As I said, they use many other kinds of humor too, which might appeal to you. JO is known for slandering his show, haircuts, nationality etc. but not too often.
It sounds more like humor in general is not for them 😅
Removed by mod
Just because someone says something you don’t agree with does not give you license to be a cunt.
Removed by mod